Instructor: Michael Pelsmajer
Office: E1 206
Office Hours: by appointment (Meaning: I am happy to meet you, but I'm not going to sit around my office, not knowing if anyone is going to show up.) To arrange a meeting, talk to me before or after class, or send an e-mail with a list of convenient times.
Office Phone: 312-567-5344 (but e-mail is better)
E-mail: pelsmajer_(AT)_iit_(DOT)_edu

Teaching Assistant: Jinyu Huang
Office Hours: Friday 4:15pm-6:15pm in E1 129
(Jinyu will take questions by e-mail as well.)
E-mail: jhuang14_(AT)_hawk_(DOT)_iit.edu
Schedule of all Math Teaching Assistants in E1 129
(They should probably be able to help, too.)

[ MATH 230 Standard Syllabus (updated 2006)]
[Spring 2012 Course information]

Homework

Suggestions for Writing up Math Homeworks (without LaTeX)
It is expected that you will check your answers to all odd-numbered problems yourself: answers are in the back of the book, while the student solution book has complete solutions for odd-numbered problems.

The book has a web site with nice extra resources. For example: Common Mistakes in Discrete Math (organized by chapter).

Daily Schedule and Assignments

Monday, January 9: Day 1, 3:15pm in Siegel Hall room 202.

Read "Spring 2012 Course information", "To the Student" (in the beginning material of the book), "Suggested Guidelines for Writing up Math Homeworks", and the beginning of "Common Mistakes in Discrete Math" (one page carefully, and then skim the Chapter 1 material).

By Wednesday, January 11:

Read, understand, and memorize alternate ways to say, "if p, then q" (page 6).

Section 1.1 (page 16-21): #9,13,14,17ab,18,20

You may need/wish to read other parts of Section 1.1. Also, it can be quite helpful to read ahead a bit to be prepared for the next class.

Due Friday, January 13:

Section 1.1: #12, 27bd, 28d, 31d

Section 1.2: #5,6, 31

No class on Monday, Jan 16

Due Wednesday, January 18:

Section 1.2: 7ab

Section 1.3: #9,10, 12,13,14, 20abcd.

All homework thus far will be collected today!

Due Friday, January 20:

Section 1.3: #7,8, 23, 25, 44

Section 1.4: #9,10, 19,20,21,22, 27,28, 31

Or if you have the 7th edition:

Section 1.4: #7,8, 23,25, 44

Section 1.5: #9,10, 19,20,21,22, 27,28, 31

Due Monday, January 23:

From Section 1.5 (6th edition) or Section 1.6 (7th edition):

Read Definition 1.

Study the first column of Table 1 (and column 2, too) until you understand why they are all valid Rules (but you can skip "Resolution").

#9,10 (but you don't need to explain using rules of inference; it's enough that you draw all the correct conclusions and that you do not draw any extra, unjustifiable conclusions)

From Section 1.6 (6th edition) or Section 1.7 (7th edition):

#1, 5, 15, 17 ("contraposition" is "contrapositive")

Due Wednesday, January 25:

From Section 1.6 (6th edition) or Section 1.7 (7th edition):

Read Examples 4 and 9.

#6, 9,10,11,12,13,14, 16, 24 (don't use "direct proof" for 24)

Homework will be collected today!

Due Friday, January 27:

• From Section 1.6 (6th edition) or Section 1.7 (7th edition):
  #26, 31, 35
• From Section 1.7 (6th edition):
  Read Examples 3,4,6,9,13 and do exercises #1,2, 5, 10, 17
  Or, from Section 1.8 (7th edition):
  Read Examples 3,4,6,9,13 and do exercises #1,2, 7, 12, 19

Due Monday, January 30:

• From Section 1.7 (6th edition):
  do exercises #11,12, 24,25, 31, and read examples 14,15
  Or, from Section 1.8 (7th edition):
  do exercises #13,14, 26,27, 33, and read examples 14,15
• From Section 2.1:
  #1,2ab,5,7,9,17 (6th edition)
  Or #1,2ab,7,9,11,19 (7th edition)

Due Wednesday, February 1:

• From Section 2.1:
  #23a, 25. (6th edition)
  #27a, 29. (7th edition)
• From Section 2.2:
  #3, 15b, 25c, 27, 29
• Homework will be collected today!

Due Friday, February 3:

• From Section 8.1 (6th edition) or 9.1 (7th edition):
  #1abcd, 6,7
  Note 1: "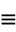 (mod 7)" is the same as 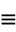₇
  Note 2: I defined "anti-symmetry" slightly differently than the book, so the answers in the back of the book may not agree.
• From Section 8.5 (6th edition) or 9.5 (7th edition):
  #2

Due Monday, February 6:

• From Section 8.5 (6th edition) or 9.5 (7th edition):
  #9, 16, 36, 40,41, 45abc

Due Wednesday, February 8:

• From Section 2.3:
  #1, 7ab, 15, and
  6th edition: #18(and if not, why not?)
  7th edition: #22(and if not, why not?)
• From Section 2.4 (6th edition): #32, 35
  Or, from Section 2.5 (7th edition): #2abcdf, 17
• Homework will be collected today!

Next up: Cardinality, Section 2.4 (6ed.) or 2.5 (7ed.). Then finish Chapter 2 Sections 3 & 4 (6th edition) or Sections 3–5 (7th edition).

Due Friday, February 10:

• From Section 2.4 (6th edition):
  #1, 5ace, 7, 13, 17d,
  33bcd, 37, 42
  (also interesting, FYI: #44–47)
• Or, from Section 2.4 (7th edition)
  1, 5ace, 7, 29, 33d
  and from Section 2.5 (7th edition):
  #3abc, 15, 28
  (also interesting, FYI: #30,37–39)

Due Monday, February 13:

• From Section 2.3:
  #9, 69abde (6th edition)
  #9, 73abde (7th edition)
• Read Chapter 3.1 and the Subset Sum Example below
• From Section 3.1:
  #1, 2, 3, 7, 8. (For #2, there's something very wrong with each algorithm: I just want you to find and describe it.)

Due Wednesday, February 15:

• Go over graded homeworks. Whatever you cannot figure out, be ready to ask me during Wednesday's class.
• Homework will be collected today!

Exam 1 will be Friday, February 17. It covers Chapters 1 and 2 (except for topics that we skipped).

Due Monday, February 20:

• Read Section 3.2. (I will discuss it in a somewhat different way, expecting that you have already read the book.)
• Next up: The Halting Problem, then Sections 3.2 and 3.3 (important stuff)

Due Wednesday, February 23:

• Section 3.2 #1, 3, 5, 9, 11 (You may use "log x < x" as a fact without proof.) There are always different possible correct choices for "C" and "k", so your answer may not be the same as the book and it may still be correct. Of course it is also possible that your answer is not the same as in the book because it is wrong.
• Optional/challenge: Section 3.1 #60 (or #64 for 7th edition)
• Homework will NOT be collected today! (Save it for next week.)

Due Friday, February 25:

• Section 3.2 #2, 10, 22, 23, 24 (7th edition: #2, 7 ,10, 8 , 28,29,30) (You may use "log x < x" and "x < 2^x" as facts without proof.)
  For each part of #2 where it is indeed O(x), you must find C,k that shows big-Oh, and you should also show a little algebra so clarifies why you chose those values. If it isn't O(x), you don't need to show anything.
  For #10, likewise but maybe more carefully. For #24, prove each part using anything from class or from the book.

Due Monday, February 27:

• Section 3.2 #7,8, 19,20,21 (7th edition: #7,8, 25,26,27)

Due Wednesday, February 29:

• Section 3.3 #7,8,9,10 (7th edition: #13,14,15, 18)
• Read "Understanding the Complexity of Algorithms" subsection of Section 3.3
• Homework (from 4 days) will be collected today!
• Next up: Number Theory

Due Friday, March 2:

• Section 3.4 #4, 8,9, 11, 17, 19 (Optional/fun: #13,15,24)
• 7th edition: Section 4.1 #4, 8,9, 15, 21, 29 (Optional/fun: #11, 17,19,38

Due Monday, March 5:

• Section 3.5 #2, 3ab, 4abcd, 5, 21, 23 (Optional/fun: #6,7, 9, 29, 33,34,35)
• 7th edition: Section 4.3 #2, 3ab, 4abcd, 5, 25, 27 (Optional/fun: #6, 11, 13, 47, 51,52,55)

Due Wednesday, March 7:

• Section 3.5 #11, 24 (7th Edition: Section 4.3 #15,28)
• Read about the Euclidean Algorithm and the Extended Euclidean Algorithm
• Homework will be collected today!

Due Friday, March 9:

• Section 3.6 #23bce
  Section 3.7 #1de, 2cg, 13 (optional/fun: #25,26)
• 7th ed: Section 4.3 #33bce, 39de, 40cg
  Section 4.4 #15 (optional/fun #31,32)
• Perhaps look at the Extended Euclidean Algorithm that I presented in class (rephrased a bit).

Due Monday, March 12:

• Section 3.7 #3, 5,6,7 or (7th edition) Section 4.4 #1, 3,4, 5ab
• Solve these:
  1. 2x 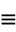7(mod 17)
  2. 12x 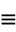15(mod 27)
  3. 19x 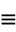4(mod 141)
  4. 8x 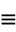2(mod 20)
  5. 34x 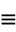77(mod 89)
• Next up: Chinese Remainder Theorem, Computer Arithmetic with Large Integers, Fermat's Little Theorem

Due Wednesday, March 14:

• Section 3.7 #18,19,20 (7th ed. #20,21,26). For #20/#26, you'll need this:
  If x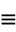y(mod m) and m=ab, then x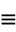y(mod a) and x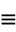y(mod b). (This is easy to prove.) By the Chinese Remainder Theorem, the reverse direction is true, so it's actually a biconditional.
• Homework will be collected today!
• Next up: Fermat's Little Theorem and RSA

Due Friday, March 16:

• Section 3.7 #28,29 (Optional/fun: #17, 46,47)
• 7th edition: Section 4.4 #38,39 (Optional/fun: 19,40, Section 4.6 #24-28)

Due Monday, March 26:

• Section 3.6 #1, 3, 5ab, 6, 9,10, 15
• 7th edition Section 4.2 #1 , 3, 7ab, 8, 11,12, 17
• Read Section 4.1 (7th ed. Section 5.1)
• Next up: Induction and Minimum Counterexamples. Material will be presented differently than in the book

Due Wednesday, March 28:

• Section 4.1 (or 7th edition Section 5.1) #5,6, 20,21, 28
  I didn't have time in class to discuss the situation where you have to prove P(n) for all n ≥ N, where N is an integer other than 1. It's the same idea, except that the base case is n=N and the inductive case is n≥ N+1. For example, for #20, the base case should be n=7 and the inductive case should be n ≥ 8.
• Homework will be collected today!

Due Friday, March 30:

• Section 4.1 (7th edition Section 5.1) #7, 10, 22,23, 45
• Read Section 4.2 (7th edition Section 5.2)

Due Monday, April 2:

• Section 4.2 (7th edition Section 5.2) #4, 7, 13,14, 17 (optional/fun: #11, 18,19)
  (Prove #4 by strong induction; you need not break it into parts abcde as they suggest.)

Due Wednesday, April 4:

• Section 4.3 (7th edition Section 5.3) #1d, 2c, 3a, 5ab, 7, 8ab, 9, 12
• Homework will be collected today!

Due Friday, April 6:

• Section 4.3 (7th edition Section 5.3) #25,26c,27ac, 43,44

Due Monday, April 9:

• Section 5.1 #1, 3,4, 6–17, 42,43, 49
• 7th edition Section 6.1 #1, 3,4, 6–17, 48,49, 55
• And read the section (as needed, or read all of it).

Due Wednesday, April 11:

• Section 5.1 #25, 27, 29, 31, 33,34,35
  7th edition Section 6.1 #27, 29, 31, 33, 35,36,37
• Homework will be collected today!
• Next up: (optional) Math Contest on Wednesday, In-class review on Wednesday, Exam 2 on Friday, Pigeonhole Principle Continued

Wednesday April 11, 12:45-1:40pm, E1 102:

IIT Math Contest This is not part of Math 230. (Math 230 students are good candidates for this).

Exam 2 will be Friday, April 13. It covers Chapters 3 and 4 (7th edition: 3,4,5) (except for topics that we skipped).

Due Monday, April 16:

• Section 5.2 (7th edition Section 6.2) #3, 5, 9, 17, 19 (Optional/fun: Read "Some elegant applications..." and/or do #10)

Due Wednesday, April 18:

• Section 5.3 (7th edition Section 6.2 6.3, oops) #1,3,5abe,7
• Homework will be collected today!

Due Friday, April 20:

• Section 5.3 (7th edition Section 6.3) #11, 13, 14, 16,17, 23, 27, 30, 33

Monday, April 23 is Menger Day. Please attend the Menger lecture instead of the usual class. And RSVP (using the link on the Menger Day web page). Also, I highly recommend the Math Club event. And the poster session.

Due Wednesday, April 25:

• Section 5.4 (7th edition Section 6.4) #3,4,5, 7,8, 13, 15, 17, 19 (Optional/fun: #21,22,... actually: Many Problems)
  Hint for 15: think about what these things count. Hint for 17: Algebraically.
• Next up: Discrete Probability

Due Friday, April 27:

• Section 6.1 (7th edition Section 7.1) #5, 9, 13, 15, 17, 21, 25a
• Homework will be collected today!

"Due" Monday, April 30:

• Optional: Section 6.2 (7th edition Section 7.2) #5, 7, 19, 23, 25, 27b
• Will not be collected

The final exam will be May 4, 10:30am-12:30pm, in the usual classroom.

I didn't talk as much about ways that an algorithm could be bad.
Here's an example that's not in the book:

Problem: Given a finite sequence of integers a1,a2,...,an, is there a non-empty subset of them whose sum equals zero?

Tiny example: For the list "3,7,-8", there are 7 non-empty subset sums:
  3+7-8, 3+7, 3-8, 7-8, 3, 7, -8,
none of which equals zero.

Attempted algorithm: For each subset, add up the elements and check if they are zero.

But! You haven't explained what order to consider the subsets! (Our example had only 3 elements, but it's less easy if you have a sequence with 10 elements - think about it).

Okay, let's say that you manage to write an algorithm that considers every non-empty subset one at a time (and is otherwise correct)...

But #2 The number of subsets to check is 2^n-1. Exponential functions grow incredibly fast, so your algorithm will be too slow: no one will have the patience to wait for it to finish when n=100 (and worse for larger n - don't even think about tackling a book-full of numbers with this algorithm).

The 6th and 7th edition are not consistent, so I will repeat and rephrase what I presented in class.

• Do the Euclidean Algorithm to find g = gcd(a,b).
  Let N be the number of times you used the division algorithm.
  (At Step N, your "r" was 0, and at Step N-1, your "r" was g.)
• Rewrite Step N-1 in the form "g = a - bq".
• Starting with i := N-2 and decreasing i by 1 each time, repeat the following:
  1. Rewrite Step i in the form "r = a - bq", and substitute it into what you have so far.
  2. Rewrite in the form g = ak + bl.
  (The last run of the loop will be with i = 1.)